1. Simple Motion
2. Accelerated Motion
3. Projectile Motion
4. Newton's Laws
5. Momentum
6. Energy
7. Heat
8. Electrostatics
9. Circuits
10. Magnetism
11. Waves1. Simple Motion
Overview
Simple motion is motion in a straight line at a constant velocity.Slides
Skills and Understanding
- Distinguish between distance and displacement.
- Distinguish between speed and velocity.
- Apply the equations for speed and velocity.
- Use the GUESS framework for problem solving.
Equations
\[ \begin{array}{ccc} \Delta x = x_{f} - x_{i} \quad \quad \quad \quad & s = \frac{d}{\Delta t} \quad \quad \quad \quad & v = \frac{\Delta x}{\Delta t} \quad \quad \quad \quad \end{array} \]Vocabulary
- Distance \(d\) is the total length of a path.
- Displacement is the change in position from the start to the end of a path. Given an initial position \(x_{i}\) and final position \(x_{f}\), the displacement \(\Delta x\) is calculated as \(\Delta x = x_{f} - x_{i}\)
- Speed is how fast something is moving. It is the rate of distance per time, and for distance \(d\) and change in time \(\Delta t\), speed \(s\) is calculated as \(s = \frac{d}{\Delta t}\)
- Velocity is the rate at which position is changing. It is calculated as \(v = \frac{\Delta x}{\Delta t}\)
1.1 Speed and GUESS
Given distance \(d\) and change in time \(\Delta t\), speed \(s\) is calculated with: \[s = \frac{d}{\Delta t}\] The GUESS method is a framework for problem solving. It stands for:- Givens — Identify the given values.
- Unknowns — Identify the unknown variables.
- Equation — Choose the appropriate equations.
- Substitute — Substitute known values into variables.
- Solve — Solve for the missing value.
Carlos drives his car a distance of \(15\) km in \(20\) minutes. What was his average speed in m/s?
↓
We can answer this question using the GUESS method.
The Givens are: \[ d = 15 \text{ km} = 15000 \text{ m} \] \[ \Delta t = 20 \text{ min} = 1200 \text{ s} \] The Unknown is: Speed \(s\).
The Equation to use is: \[ s = \frac{d}{\Delta t} \] We Substitute to get: \[ s = \frac{15000 \text{ m}}{1200 \text{ s}} \] And Solve to find: \[ s = 12.5 \text{ m/s} \]
The Givens are: \[ d = 15 \text{ km} = 15000 \text{ m} \] \[ \Delta t = 20 \text{ min} = 1200 \text{ s} \] The Unknown is: Speed \(s\).
The Equation to use is: \[ s = \frac{d}{\Delta t} \] We Substitute to get: \[ s = \frac{15000 \text{ m}}{1200 \text{ s}} \] And Solve to find: \[ s = 12.5 \text{ m/s} \]
1.2 Distance, Displacement, Speed, Velocity
Distance refers to the total length of a path, whereas displacement refers to the distance from the start to the end of a path. For example, if I walk \(6\) m forward and then \(10\) m backward, my distance traveled is \(16\) m while my displacement is \(-4\) m (that is 4 m behind where I started). Note that distance can never be negative but displacement can.
Speed is calculated using distance, \(s = \frac{d}{\Delta t}\), so it too can never be negative. Velocity on the other hand is calculated with displacement, \(v = \frac{\Delta x}{\Delta t}\), so it can be negative. Consider a car driving backward \(20\) miles in an hour. We would say that it's velocity is \(-20\) mph, but it's speed is \(20\) mph.
Juan went biking from home straight to his friend's house 843 meters away. He then biked back towards home 325 meters before taking a break. Juan did this all in 9 minutes. What was Juan's average speed in m/s, and what was his average velocity in m/s?
↓
The Givens are:
\[ \Delta t = 9 \text{ min} = 540 \text{ s} \]
Adding the lengths to get total distance, we have: \[ d = 843 + 325 = 1168 \text{ m} \]
We can say his initial position is: \[ x_{i} = 0 \text{ m} \]
We can find his final position from home: \[ x_{f} = 843 - 325 = 518 \text{ m} \]
The Unknowns are: Speed \(s\) and velocity \(v\).
The Equations to use are: \[ \begin{array}{cc} s = \frac{d}{\Delta t} \quad \quad & v = \frac{\Delta x}{\Delta t} = \frac{x_{f} - x_{i}}{\Delta t} \end{array} \] We Substitute to get: \[ \begin{array}{cc} s = \frac{1168 \text{ m}}{540 \text{ s}} \quad \quad & v = \frac{518 \text{ m} - 0 \text{ m}}{540 \text{ s}} \end{array} \] And Solve to find: \[ \begin{array}{cc} s = 2.16 \text{ m/s} \quad \quad & v = 0.96 \text{ m/s} \end{array} \]
The Equations to use are: \[ \begin{array}{cc} s = \frac{d}{\Delta t} \quad \quad & v = \frac{\Delta x}{\Delta t} = \frac{x_{f} - x_{i}}{\Delta t} \end{array} \] We Substitute to get: \[ \begin{array}{cc} s = \frac{1168 \text{ m}}{540 \text{ s}} \quad \quad & v = \frac{518 \text{ m} - 0 \text{ m}}{540 \text{ s}} \end{array} \] And Solve to find: \[ \begin{array}{cc} s = 2.16 \text{ m/s} \quad \quad & v = 0.96 \text{ m/s} \end{array} \]
1.3 Position versus Time Graphs
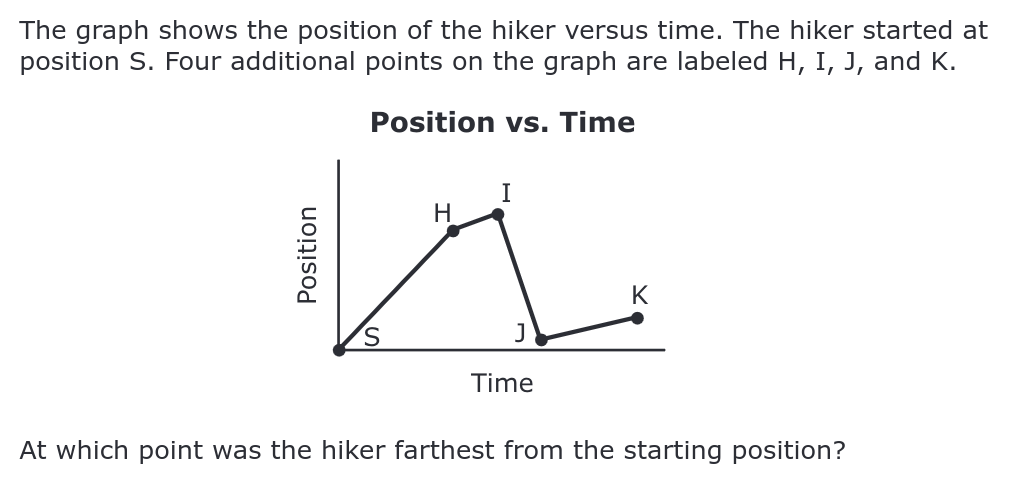
Source: 2022 MCAS
↓
The \(y\)-axis in the graph represents the position of the hiker.
The starting point \(S\) is at the origin, and the position that is furthest from the origin is point I.
A bit of nuance: it would be a mistake to choose point I only because it is the "highest" up the graph. The reason that point I is the correct answer is because it is furthest, and happens to be a positive value. If there were a point further away but in the negative direction, then the answer would be the "lowest" point down.
A bit of nuance: it would be a mistake to choose point I only because it is the "highest" up the graph. The reason that point I is the correct answer is because it is furthest, and happens to be a positive value. If there were a point further away but in the negative direction, then the answer would be the "lowest" point down.
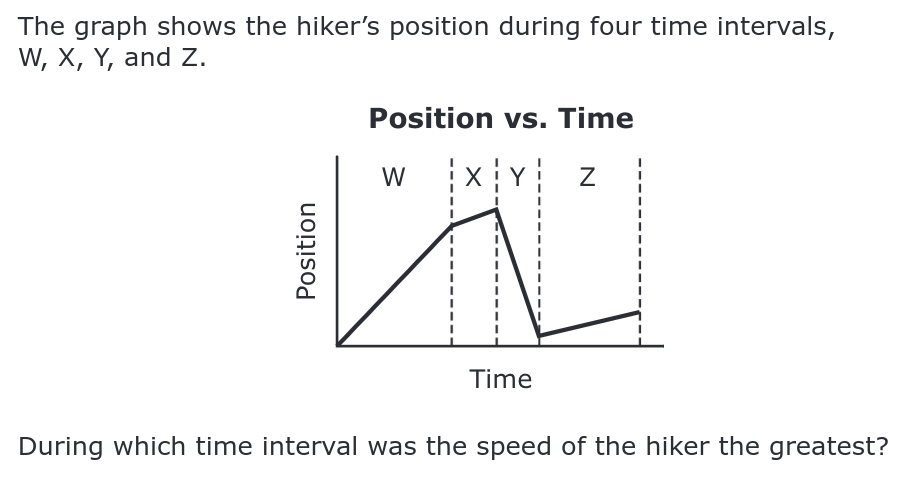
Source: 2022 MCAS
↓
In a position-versus-time graph, slope is the rate of change of position (velocity).
The steepest slope represents the greatest speed.
In the graph above, the slope is steepest over time interval Y.