9. Circuits

Overview

Slides

Skills and Understanding

Apply Ohm's Law to calculate voltage, current, and resistance.
Analyze series and parallel circuits, including calculating resistance of complex arrangements of resistors.
Determine the power used in a circuit or in components of a circuit.

Equations

\[ \begin{array}{cc} V = IR \quad \quad \quad \quad P = IV \\ R = R_{1} + \dots + R_{n} \quad \quad \quad \quad \frac{1}{R} = \frac{1}{R_{1}} + \dots + \frac{1}{R_{n}} \\ \end{array} \]

Vocabulary

Voltage \(V\) is an electric potential, measured in volts (V).
Current \(I\) is the flow of electric charge, measured in amperes (A) or "amps".
Resistance \(R\) is an opposition to the flow of current, measured in ohms (\(\Omega\)).
Power \(P\) is the rate at which electrical energy is transferred within a circuit, measured in watts (W).
A Series circuit is one in which the components are arranged one after another, where the output of one component leads to the input of the next.
A Parallel circuit is one in which the components are arranged so that their inputs are connected and their outputs are connected. The diagram of such an arrangement shows the components to be parallel to one another.

9.1 Intro to Circuits

An electric circuit is a closed loop through which electric current can flow. It consists of electrical components including resistors, capacitors, switches, and power sources like batteries. Three fundamental properties of circuits are current, voltage, and resistance.

Current (I) refers to the flow of electric charge, and is measured in amperes (A). It is the rate of change of charge per time, \(I = \frac{\Delta q}{\Delta t}\), where \(\Delta q\) is the change in charge.
Voltage (V) is an electric potential measured in volts (V), and can be thought of as a pressure that "pushes" on charge to create current. Increasing voltage increases current.
Resistance (R) is an opposition to the flow of current, measured in ohms (\(\Omega\)). Increasing resistance decreases current.

The three are related by Ohm's Law, which is usually written as: \[V=IR\] If we rearrange Ohm's Law as \(I=\frac{V}{R}\), we see that current is directly proportional to voltage and inversely proportional to resistance.

Circuit Diagrams

The circuit diagram below depicts a circuit with two components: a voltage source (battery) on the left, and a resistor on the right. They are connected by wire (lines).

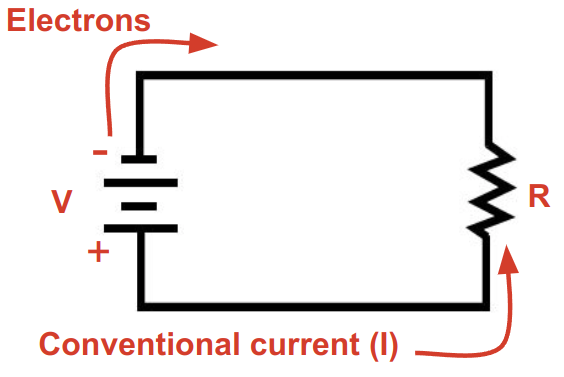
We analyze current as "moving" in the positive direction, even though physically the positive charges are stationary while electrons are flowing from the negative (-) side of the battery toward the positive (+) side.

Find the current in the circuit below:

↓

We use Ohm's law, and note that 10 k\(\Omega\) is 10 kilo-Ohms, or 10,000 Ohms. \[V = IR\] \[I = \frac{V}{R}\] \[I = \frac{3}{10000} = 0.0003 A \] The answer could also be written as 0.3 mA (milliamps). Current is usually quite small and is often expressed in mA.

9.2 Series Circuits

A series circuit is one where the components are connected in a series. That is, one after another so that the output of one component leads to the input of the next.

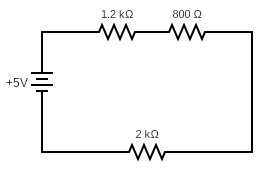
Equivalent Resistance

Imagine replacing all of the resistors in the circuit above with a single resistor with the same overall resistance. We call this equivalent resistance. For a series of resistors \(R_{1}\), \(R_{2}\), ..., \(R_{n}\), the equivalent resistance is the sum of all thre resistances: \[R = R_{1} + R_{2} + \dots + R_{n} \] For the circuit above we would get \(R = 1200 + 800 + 2000 = 4000 \Omega \)

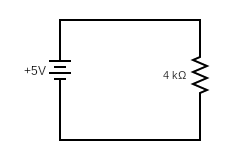
Find the current in the circuit below:

↓

First we find the equivalent resistance: \[R = 100 + 200 + 500 = 800 \Omega\] We use Ohm's law, \[V = IR\] \[I = \frac{V}{R}\] \[I = \frac{24}{800} = 0.03 A \]

9.3 Parallel Circuits

9.4 Power

Electric power is the rate at which energy is used by a circuit or circuit component. Power is measured in Watts \(W\), which is equivalent to Joules per second. Power is the product of current and voltage, \[ P = IV \] We can find the total power in a circuit, or the power used by individual components.

Find the power used by each resistor in the circuit below:

↓

We know from a the exercise above that the total current is: \[I = 0.03 A \] The power is \[P=IV\] for each component, where \(I\) = 0.03 A and V is the voltage drop across a given resistor. Given that the voltage drop is found with \(V=IR\), we can find the \(V\) for each component, or substitute into the power equation to get: \[ P = IV = I (IR) = I^{2} R \] Then the power for each resistor would be: \[ P_{1} = (0.03)^2 \cdot 100 = 0.09 \text{ W} \] \[ P_{1} = (0.03)^2 \cdot 200 = 0.18 \text{ W} \] \[ P_{1} = (0.03)^2 \cdot 500 = 0.45 \text{ W} \]