6. Energy

Overview

Slides

Skills and Understanding

Determine work done by a force on an object.
Determine work as the change in kinetic energy.
Calculate potential energy.
Apply conservation laws to determine the transfer of energy.

Equations

\[ \begin{array}{cc} W = F d \cos(\theta) \quad \quad \quad \quad E_{k}=\frac{1}{2}mv^{2} \\ \sum W = \Delta E_{k} \quad \quad \quad \quad E_{p} = mgh \\ \end{array} \]

Vocabulary

Energy is the ability to do work.
Gravitational Potential Energy is the potential energy of an object at a certain height due to gravity, \(E_{p}= mgh\) where \(h\) is the height of the object.
Kinetic Energy is the energy of motion, \(E_{k}= \frac{1}{2}mv^{2}\)
Work is the mechanical transfer of energy. Work by a force on an object is calculated as the product of the component of that force in the direction of motion and the distance moved by that object, \(W=F d \cos(\theta) \) where \(\theta\) is the angle between the applied force and the direction of motion.
Work-Energy Theorem states that the sum of work on an object is equal to the change in kinetic energy, \(\sum W = \Delta E_{k}\)

6.1 Work

Work is a measure of the transfer of energy that occurs when an applied force results in the displacment of an object. \[W = F d \cos(\theta) \] where \(\theta\) is the angle between the force \(F\) and the direction of motion of the object.

You push horizontally on a large box with a force of 38 N. If the crate moves a distance of 3.7 m in the direction you are pushing, how much work did you do on the crate?

↓

\(F = 38\) N and \(d = 3.7\) m. Since we are pushing in the direction the crate is moving, \(\theta=0 ^{\circ}\), and we have \[W = F d \] \[W = 38 \cdot 3.7 = 140.6 J \]

To move a crate, you push on it with a force of 32 N at an angle of \(12^{\circ}\) above the horizontal. If you move the crate 8 m, how much work did you do on the crate?

↓

\[ W = F d \cos(\theta) \] \[ W = (32) (8) \cos(12^{\circ}) = 250.4 J \]

6.2 Kinetic Energy and Work

Kinetic energy is the energy an object possesses in the form of its motion. \[ E_{k} = \frac{1}{2}mv^{2} \] Work can be calculated by finding the change in kinetic energy, \[ W = \Delta E_{k} \]

A 44 kg wagon is moving with velocity 4 m/s. If you apply a force to the wagon, increasing its velocity to 7 m/s, how much work did you do on the wagon?

↓

\[ W = \Delta E_{k} = E_{kf} - E_{ki} = \frac{1}{2} m v_{f}^2 - \frac{1}{2} m v_{i}^2 \] \[ W = \frac{1}{2} (44) (7)^2 - \frac{1}{2} (44) (4)^2 = 726 \text{ J} \]

6.3 Gravitational Potential Energy

The potential energy of an object (due to gravity) is a measure of energy an object has in its potential to fall. The higher up an object is, or the more massive it is, then the more gravitational potential energy it has. \[ E_{p} = mgh \]

6.4 Conservation

Mechanical energy \(E_{M}\) is the total sum of kinetic and potential energy, \[ E_{M} = E_{p} + E_{k} \] When no energy is lost to friction, sound, etc., the mechanical energy remains constant, even as potential and kinetic energies trade off.

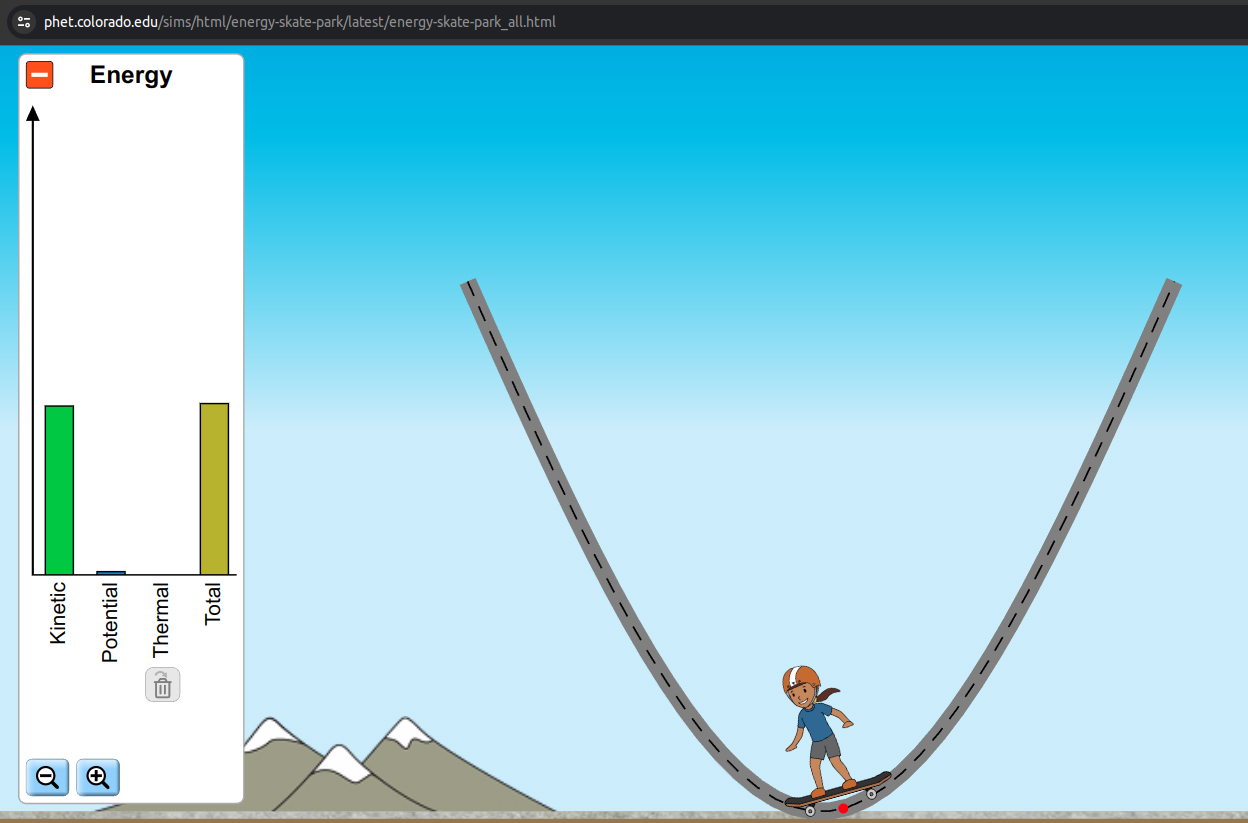
Visit the PhET energy skate park. Let the skater loose on the track and click the green + to see the energy graph. Notice that the total energy remains constant, the potential energy is maximized when the skater is higher off the ground, and the kinetic energy is maximized when the skater is going fastest at the bottom of the ramp.